ca. 30 Sekunden, etwa 2,1 MB
Der Vortrag über die Bohmsche Mechanik (auch De-Broglie-Bohm-Theorie) entstand im Rahmen des Seminars "Interpretation der Quantenmechanik" 2010 an der Goethe Universiät in Frankfurt.
Von den meisten Physikern wird heutzutage die Kopenhagener Interpretation der Quantenmechanik bevorzugt, welche den Teilchen keine Bahnen, sondern nur Wahrscheinlichkeitsverteilungen für Orte und Impulse (und weiteren Observablen) zu. Erst bei der Messung wird dann ein Wert zufällig mit entsprechender Wahrscheinlichkeit ausgewählt. Dadurch wird bei ein und demselben Versuchsaufbau immer ein anderer Wert gemessen. Bei ganz vielen Messungen nähert man sich der Wahrscheinlichkeitsverteilung. Dadurch wird der von Newtonschen Mechanik vertretene Determinismus aufgegeben.
Die Bohmsche Mechanik ist eine andere mögliche Interpretation der Quantenmechanik, bei der den einzelnen Teilchen nun wie in der Newtonschen Mechanik, Bahnen zugeordnet werden können. Die beobachtete Zufälligkeit ist hier nicht einem Messprozess geschuldet sondern liegt an der Unkenntniss der Anfangsbedingungen, welche sich sehr schnell so stark vergrößern, dass man sie beobachten kann. Dies ist vergleichbar mit der der statistischen Physik (Thermodynamik).
Obwohl sich die Bohmsche Mechanik und die Kopenhagener Interpretation fundamental in ihrem Weltbild unterscheiden, sind sie mathematisch gesehen sehr nahe. Beide verwenden die Schrödingergleichung und dieselben Operatoren. In der Bohmschen Mechanik kommt noch eine Führungswellengleichung hinzu, mit der man Bahn bestimmen kann. Das führt dazu, dass beide Interpretation exakt die gleichen Vorhersagen machen und damit (wenn man sich auf den Geltungsbereich der Kopenhagener Interpretation zurückzieht) nicht unterscheidbar sind.
Im folgenden wurden ein paar typische Experimente der Quantenmechanik für die Bohmsche Mechanik simuliert. Das Programm habe ich selbst in C++ / Qt 4 geschrieben. Es simuliert zunächst die zeitabhängige Schrödingergleichung auf einem zweidimensionalen Gitter numerisch, wobei jedem Gitterpunkt eine Potentialstärke zugewiesen wurde. Dieser Schritt simuliert die Wellenfunktion, wie sie auch in der Kopenhagener Interpretation verwendet wird.
In einem zweiten Schritt wird die Führungsgleichung numerisch gelöst, welches numerisch leider nicht ganz so stabil ist, weshalb ab und zu "Ausreißer" zu sehen sind.
Die Berechnung geschieht nicht in Echtzeit, da der Algorithmus nicht so schnell ist (die Berechnungen sind aber noch recht "human", ich habe für die Beispiele auf dieser Seite weniger als eine Minute benötigt). Das Ergebnis kann dreidimensional dargestellt werden, wobei die dritte Dimension die Potentialstärke, bzw. die Amplitude der Wellenfunktion angibt und in der Zeit hin- und hergespult werden.
Ich habe vor, das Programm hier im Quelltext zu veröffentlichen, wenn ich etwas Zeit habe, es zu vervollständigen.
Update Oktober 2016: Leider habe ich noch keine Zeit gefunden, das Programm so zu vervollständigen, dass es "vorzeigbar" wäre.
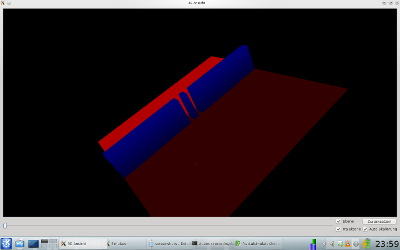
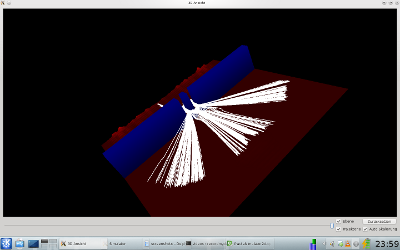
Der Doppelspalt gehört zu den Klassikern in der Quantenmechanik und wurde hier durch einen Potentialwall simuliert, der zwei Löcher besitzt und auf den eine ebene Welle auftritt. Man kann grob erkennen, dass die Bahnen in der oberen Bildhälfte durch den oberen Spalt und die unteren Bahnen durch den unteren Spalt führen.
| Aufbau |  |
| Bahnen |  |
| Video | Video im Ogg Format ca. 30 Sekunden, etwa 2,1 MB |
Der Tunneleffekt wird hier für drei verschiedene Potentialhöhen gezeigt. Es treffen auf alle Potentiallwälle das gleiche Teilchen in Form eines Gausspaketes auf. Je höher das Potential ist, um so geringer ist der Anteil an Bahnen, die das Potential durchtunneln können.
| Aufbau | 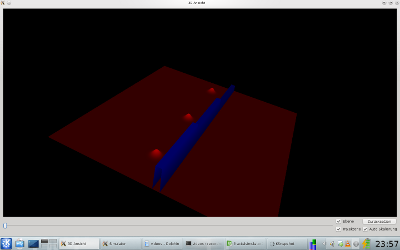 |
| Bahnen | 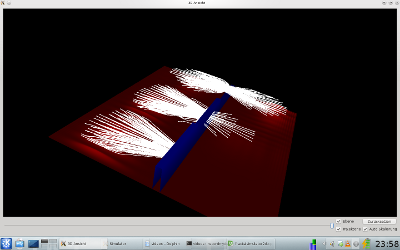 |
| Video | Video im Ogg Format ca. 70 Sekunden, etwa 10,3 MB |
Das Interferometer besteht aus zwei Spiegeln und zwei Strahlteilern. Die Spiegel werden durch hohe Potentialwände
realisiert, während die Strahlteiler durch kleinere Potentialwände simuliert werden. Hierbei wird der Tunneleffekt
ausgenutzt.
Der einlaufende Strahl (ebene Welle) wird zunächst aufgeteilt, an den Spiegeln reflektiert und dort wieder
vereint. Das Interferometer ist so gebaut, dass die Strahlen an einem der Ausgänge konstruktiv und am anderen destruktiv
interferieren.
Plaziert man nun ein Hinderniss in einem der beiden Strahlen, so kommt es am Ausgang nicht zur Interferenz und es sind
Teilchen an beiden Ausgängen zu messen.
| Aufbau | 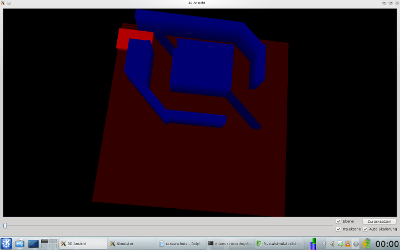 |
| Bahnen | 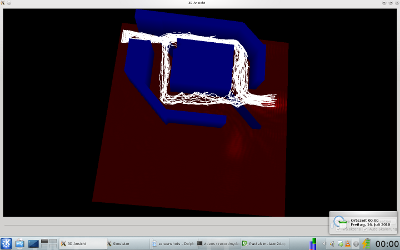 |
| Bahnen mit Hinderniss | 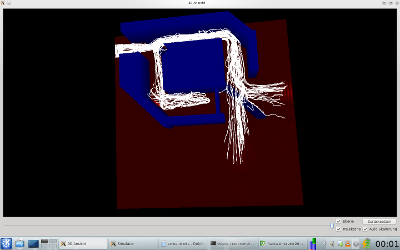 |
| Video | Video im Ogg Format ca. 135 Sekunden, etwa 13,6 MB |
Impressum | Datenschutzerklärung | [*]: externer Link | thilo.ackermann@gmail.com